Time is one of humanity’s greatest blind spots

Tags

conservation biology, conservation paleobiology, extinction, paleontology

Humanity’s shortsightedness around time creates major constraints on modern conservation.

Looking south to the upper Gulf of California and the Colorado River delta

Many years ago, in the late 1990’s, I had the privilege and pleasure of working with Karl Flessa at the University of Arizona. I had gone there as a researcher to participate in Karl’s Gulf of California project, as one component of the project involved a group of marine bivalves (clams) on which I was an expert. The goal of the project was to assess the changes that had taken place, and were ongoing, in the northern Gulf after damming of the Colorado River. By the time that we were working there, it had been several decades since freshwater flowed into the former river delta in any appreciable volume. Almost all the water, which is generated largely from snowmelt in the Rocky Mountains, is now utilized by the western United States and Mexico. The changes were profound; increases of salinity, increased tidal influence, changes of dominant species and so on, much of which has been documented by the aptly named CEAM (El Centro de Estudios de Almejas Muertas). This was my first introduction to the then nascent field of conservation paleobiology, which has since developed into a major subdiscipline of the paleobiological sciences. The community is now centered around the Conservation Paleobiology Network, a great resource for learning more. The goal of conservation paleobiology is to apply paleontological and geological work, primarily of past species and ecological systems, to understanding, conserving, and regenerating current ecological systems.

System diagram of a historical N. Pacific kelp forest (Roopnarine et al., 2022).

Roxanne Banker, Scott Sampson and I published a conservation paleobiology paper last year in which we proposed a new approach to both conservation biology and paleobiology, the Past-Present-Future (PPF) strategy. The idea is to use conservation paleobiology as a rubric to combine diverse data streams, e.g. fossils, historical data, indigenous knowledge, with mathematical modeling to reconstruct historical and current systems, and apply the results to conservation in the near-term future. The paper focused on the role of an extinct sirenian (manatees, dugongs), Steller’s Sea Cow, in the dynamics of North Pacific giant kelp forests. Those forests have been devastated during the past decade by marine heat waves, and the loss of sunflower sea stars, a major predator of the kelp-consuming purple sea urchin. We found that kelp forests would have, under many circumstances, been more resilient to those disturbances in the presence of the sea cow. Unfortunately, the sea cow was driven (consumed) to extinction in the early to mid-18^th century, shortly after its discovery by Russian commercial hunters.

Recently Scott and I have published an opinion piece in Scientific American magazine, We Need to Think about Conservation on a Different Timescale, in which we more broadly advocate for the PPF approach and conservation paleobiology. The mathematical modeling of historical and ancient ecosystems can be extremely challenging, but as we showed in our paper, and argue in this opinion article, it is both feasible and bears great potential. As we state in the closing of the article:
“We are all characters in an epic story that has been unfolding for millions upon millions of years. The decisions we make today will shape how the future unfolds. It’s high time we embraced our role in this ever-evolving drama and established vital through lines from past to future.“

Sampson, S. D. and P. D. Roopnarine 2023. We Need to Think about Conservation on a Different Timescale. Scientific American.
Roopnarine, P. D., R. M. Banker and S. Sampson. 2022. Impact of the extinct megaherbivore Steller’s sea cow (Hydrodamalis gigas) on kelp forest resilience. Frontiers in Ecology and Evolution. https://doi.org/10.3389/fevo.2022.983558.

Why does ecosystem collapse matter?

Tags

ecosystem collapse, extinction

Collapse of the Aral Sea ecosystem (NASA)

I just received an interesting query from a journalist who is working on the apparently imminent collapse of the Sonoran Desert ecosystem. The question was, “Why does it matter if the Sonoran ecosystem collapses?” I found this to be very interesting because, in contrast to “what does ecosystem collapse mean”, the question was about why it matters. This is a very good question as potentially takes us beyond the scientific meaning, and is asking more broadly, why should we care? I realized that I actually don’t have a certain answer for this, but I tried to provide a brief and thoughtful response, which I now include here…

“Well, that’s actually a very good question. There’s a difference I guess between what it means, and why it matters. I’ll give you my take on it.

An ecosystem is something that humans define (e.g. see https://www.cambridge.org/core/books/ecosystem-functioning/148A9BB94FCCFD3F4AE23B675FB6511E), generally as the assemblage of species and their environment in a particular place, and at a particular time. An ecosystem is collectively all those species and their interactions with each other and the environment, and the processes that emerge from those interactions. It is the processes, such as energy flow or nitrogen fixation, that sustain the system. So there is this feedback loop, where species create processes, and the collection of those processes create the conditions necessary for the species to persist. The collapse of an ecosystem is a breakdown of that loop, where because of species losses or environmental changes, or both, some species no longer contribute to a particular process, or a process that is necessary for the persistence of a species is no longer sufficient or present. The result is a disruption of species functioning, accompanied by the decline or extinction of species, and a disruption of environmental processes.

Why does that matter if the Sonoran system collapsed? I think that it depends a bit on who you ask. It matters from the biodiversity perspective, because of the loss or increased risk of loss of species. Many people place great value on the intangible value of biodiversity. Biodiversity is the foundation of ecosystem resilience, and changes to that biodiversity changes ecosystem resilience. And resilient ecosystems provide ecosystem services, which are the benefits that human societies gain from ecosystem functioning, such as oxygen, clean water, biological resources, etc. So in addition to the loss of a rather unique system of species, and their evolutionary potentials/futures, we will also reduce the benefits that societies connected to the Sonoran system are dependent upon. And that is a cascading consequence, of course, as those societies then will look elsewhere for those benefits.”

COVID-19, Economics, Tipping Points – Composition and Complexity

Tags

complexity, COVID-19, economics, food webs, Network theory, networks, real world networks

Previous posts in this series:
1. COVID-19, Economics, Tipping Points – Part I
2. COVID-19, Economics, Tipping Points – Socioeconomic Networks
3. COVID-19, Economics, Tipping Points – All Models are Lies
4. COVID-19, Economics, Tipping Points – Simulating an Outbreak

5. COVID-19, Economics, Tipping Points – Economic Structure and Diseas

Roopnarine, P. D., M. Abarca, D. Goodwin and J. Russack. 2023. Economic cascades, tipping points, and the costs of a business-as-usual approach to COVID-19. Frontiers in Physics. 11:1074704. doi: 10.3389/fphy.2023.1074704

And…the blog is back after a little unplanned-for break due to COVID-19. After having successfully avoided the disease for three years, my luck finally ran out. Note: vaccination and Paxlovid work! But it still sucked.

Structural Complexity

Functional network of a 250 million year old forest ecosystem. Each node contains species that perform specific functions in the food web (Roopnarine et al., 2019).

One of the remarkable features that is emerging from the study of ecosystems is that they, like many other types of complex systems, can be remarkably persistent–they last for considerable periods of time. What paleoecologists have been learning is that ecosystems have somewhat definable durations, “lifespans” if you will, over which they will arise and eventually disappear or transform. More intriguingly, if we describe an ecosystem according to its functions, or the various roles that species are performing in the system, then both the set of functions and the processes that they form through their interactions, tend to last much longer than the species that are performing those functions. In other words, species may come and go because of evolution (or immigration) and extinction, but the structure of the system remains the same. My personal favourite demonstration of this comes from a study of mammalian assemblages from the Iberian Peninsula spanning a time period of about 20 million years ago almost to the present^1,2. In that story, waves of mammals would sweep into the peninsula across the Pyrenees Mountains and replace resident species, but would in no way alter the way in which the ecosystem was structured. That happened only a few times, driven by major changes of climate. Each paleoecosystem lasted on average 10 million years, whereas species tended to persist only 1-2 million years.

In yet another study, this one by myself and colleagues of an ancient ecosystem 260-245 million years ago in today’s Karoo Basin of South Africa, we described a situation very similar to the later Iberian one–species came and went in an otherwise structurally unchanging system. Unchanging, that is, until a mass extinction struck at 251 million years. The end Permian mass extinction, the most severe known in the fossil record, eventually undid the Karoo system. What followed was a succession of short-lived systems, and it wasn’t until about 7 million years later that a new and persistent system arose. We were able to determine that great persistence, or lack of it, depends on three systems characteristics: the types of ecological functions present in a system, the network of interactions among those functions, and how the total number of species in the system (species richness) is divided up among those functions (see above figure). We referred to this collection of traits as the “structural complexity” of a system.

Socioeconomic systems and structural complexity

These “cheese wedge” figures were introduced in the previous post. They illustrate the responses of a socioeconomic system (SES) to a range of outbreak intensities of COVID-19, with both the depth and colouration of the wedges indicating the extent to which employment is expected to decline according to our CASES model; the deeper the wedge, the greater the loss of employment. We connected these results of SES-COVID dynamics to SES structure by analyzing the structural complexity of the California SESs. If you recall, the network of interactions between industrial sectors in the SESs is complete–all sectors interact with each other. This stands in contrast to ecosystems, where interactions among functions are more sparse, and in fact dense functional networks would probably be disastrous (see Red Queen for a Day). The upshot is that we need consider only a single feature of structural complexity in the SESs: how the total number of workers is divided among industrial sectors.

There is a total of fifteen sectors, and not only would we like to compare how a sector varies among SESs, for example, how many people are employed in Manufacturing in Los Angeles versus Fresno, but we also wish to account for how sectors vary with regards to other sectors, both within and between SESs. For example, do SESs with large Financial Services sectors also have large Health and Education sectors? And, most importantly, is there any relationship between the structural complexity of an SES and its predicted response to an outbreak of COVID? We turned to a mathematical technique called principal components analysis (PCA) to answer these questions. In our case, a PCA analysis uses both the sizes of sectors, and the relative sizes of sectors–what fraction of workers are in each sector–to compare SESs. It works like this. Imagine that we plotted our SESs on axes according to sector sizes. The next figure shows the SESs plotted in 2-dimensional spaces, where each dimension represents a sector, and each point is an SES, the location of which depends on how large the sectors are in that SES (the numbers are relative to the mean value of all the SESs, in tens of thousands). Pulling all the sectors together, we can imagine each SES to be a distinct point in a 15-dimensional space. We can imagine this in an abstract way, but as humans we can “typically” imagine no more than 3-dimensional spaces.

One of the great advantages of techniques such as PCA is that they can usefully condense or summarize variation in many dimensions into new dimensions by taking advantage of the fact that the original dimensions are correlated–back to the notion that larger Financial Services sectors co-occur with larger Health and Education sectors. And because the new dimensions, known as principal components, account for correlation among the original ones, they capture more of the original variation in fewer dimensions. The hoped for result is that we can then begin to view our data in a space that is more manageable, in our case, fewer than 15 dimensions.

Here is the result of the PCA. It’s a busy figure, so let’s unpack it. First note the arrows that are pointing in several different directions. These are our original dimensions, or industrial sectors, and more than 90% of their variation is now captured by only two principal components (the x and y axes). Now look at our data points, the SESs. They are scattered in directions that indicate the relative sizes of the sectors in their structures. For example, the Agriculture (Farming) sector is relatively larger in Fresno than it is in San Francisco or Los Angeles. In general, there are two contrasting directions: Agricultural dominance versus all the other sectors, captured by Principal Component 1 (x axis), and goods-producing versus services-providing sectors (e.g. Mining and Logging versus Financial Services). The arrangement, or “ordination” of the SESs produced by the PCA is easily relatable to the reality of the communities that they represent, and we have great confidence that the results of this analysis gives us an insightful comparison of the structural complexities of the SESs.

Now, here’s the really interesting part. Alongside each point we plotted the cheese wedges for each SES, showing how our model predicts it would respond, employment-wise, to an economically unmitigated outbreak of COVID. The striking feature is that the severity of impact diminishes as we move from left to right in the figure (the wedges become smaller). The SESs also increase in size as we move in the direction, leading toward the behemoth Los Angeles SES, but it isn’t size per se that is driving the pattern; its a bit more subtle. It is the composition of the SESs. An SES that is smaller tends to have a relatively larger Agriculture sector, and goods-producing sectors in general, such as Manufacturing, whereas larger SESs tend to have relatively larger services sectors, such as Financial Services, and Leisure and Entertainment. Some of the contrast between California’s inland and coastal communities is also reflected, although there are exceptions, such as Oxnard’s location to the far left. And in the next post we’ll discuss an additional factor, and that is the age of the workforce in an SES, because remember, age and severity are related when it comes to COVID-19.

The main message of the analysis is this: Californian SESs would respond differently to COVID outbreaks in the absence of economic shutdowns, and in a manner based on their sizes, geography, and how their workforces are divided among industrial sectors. In the next post we will explore exactly how those differences would have been predicted to play out according to the CASES model.

References

1. Blanco, F., Calatayud, J., Martín-Perea, D. M., Domingo, M. S., Menéndez, I., Müller, J., … & Cantalapiedra, J. L. (2021). Punctuated ecological equilibrium in mammal communities over evolutionary time scales. Science, 372(6539), 300-303.
2. Roopnarine, P. D. and R. M. W. Banker. 2021. Perspective: Ecological stasis on geological timescales. Science 372:237-238.

COVID-19, Economics, Tipping Points – Economic Structure and Disease

Tags

Network theory, networks, real world networks, simulations

Previous posts in this series:
1. COVID-19, Economics, Tipping Points – Part I
2. COVID-19, Economics, Tipping Points – Socioeconomic Networks
3. COVID-19, Economics, Tipping Points – All Models are Lies
4. COVID-19, Economics, Tipping Points – Simulating an Outbreak

Roopnarine, P. D., M. Abarca, D. Goodwin and J. Russack. 2023. Economic cascades, tipping points, and the costs of a business-as-usual approach to COVID-19. Frontiers in Physics. 11:1074704. doi: 10.3389/fphy.2023.1074704

I had the great pleasure of giving a presentation last week about this COVID-19 and economics work to a very interesting research group, the ASPIRE (Adaptive Social, Psychological, and Information Response to Emergencies) Collaboratory. It’s a great group of very interesting people! Assembling the presentation really forced me to think about the entire narrative thread of what we did in our own study, and I was able to align the pieces better into a good storyline. In the previous blog post I explained the mathematical models underlying our counterfactual exploration, but the first interesting result did not actually come from the simulation of any particular SES (socioeconomic system) following outbreak of COVID-19 in early 2020, but actually from considering how an SES would respond to any sort of COVID-19 outbreak. What is “any sort” referring to? It means that early in 2020, the impact of COVID-19 varied greatly across societies and geography. Much of this variation can be tied to the timing of the disease’s arrival to a particular place. In general, the earlier the outbreak, the more severe were the consequences. This was true of the first hot spot in Europe, northern Italy, as it was of the first hot spot in the United States, New York City (see the graphic below). It must also have been true in Wuhan, the probable ground zero of COVID-19, and other large Chinese cities to where people would have traveled extensively before it was apparent that an epidemic was underway. All this variation created not only uncertainty about the nature of the disease, but also variation in the severity of initial outbreaks.

April 2020. Source: Pew Research Center analysis of COVID-19 Data Repository from the Johns Hopkins University Center for Systems Science and Engineering as of Dec 3, 2020. See methodology for details. “The Changing Geography of COVID-19 in the U.S.”

This uncertainty can be expressed as variation of the “infection rate”, the in the SIR model or, in our case, the estimate of the initial infection rate of an outbreak, the notorious R₀ (pronounced R nought for my American friends). R₀ is generally specific to particular circumstances defined by such factors as geography, geographic connectedness, and local factors such as population size, individual movements, and of course the contagiousness of the disease itself. In the case of COVID-19, those estimates varied roughly between 2 and 4, which are the number of persons expected to be infected by an infected person in a given time period. R₀ less than 1 means that the disease will die out, while R₀>1 means that it will spread through the population. The actual estimates for our Californian SESs at the beginning of March, 2020 ranged from a low of 1.59 for San Jose-Sunnyvale-Santa Clara, to a high of 2.63 for Stockton-Lodi (obtained from the California Department of Public Health’s California COVID Assessment Tool, CalCAT).

We were interested in the general question of how each SES would respond economically across a range of R₀ values, given the counterfactual situation where the economies would remain open. To do this, we simply simulated the model (see this post), relating outbreaks of COVID-19 to losses of employment, for each SES at R₀ ranging from 1.01-6, for 150 days. This would allow us to both see what the model predicts in general, as well as compare SESs. The results are best understood by looking at the following three dimensional plot. The axes at the base are your conventional x and y axes, with x representing the day of the simulation, and y the value of R₀. The z or vertical axis shows the normalized level of employment in the SES, normalized meaning that a value of 1 represents the original employment level on March 1, 2020, and 0 meaning a complete loss of the workforce. The surface of the plot itself therefore shows the level of employment on any given day at any value of R₀.

The figure here is for the Los Angeles-Glendale-Long Beach SES, and if you look closely you will see that there are actually two surfaces plotted. The upper transparent grey surface plots the fraction of employees lost directly to infection by COVID-19, which would result in either death or illness so severe as to lead to a loss of employment. Note that the surface is basically flat both early in time, and at low values of R₀. However, as either time passes and the disease spreads, or the infection rate increases, or both, there is then a rapid decline of employment–that noticeable dip of the surface. It eventually levels off again as the disease has peaked. There is a second and lower surface, the colourful one. That surface shows the TOTAL loss of workers, that is, workers lost directly to infection (the grey surface), PLUS workers who subsequently lose their jobs because productivity and demand in their industrial sector, basically economic activity, are reduced by the diminished workforce. This is the economic cascade, and it will always be at least as severe as the disease-only cascade. This result therefore is the estimate that we have been seeking–the number of employees that would be lost as a consequence of maintaining an open economy during an outbreak of COVID-19.

Now, here’s where it gets really interesting. Let’s repeat that exercise, but this time with a different SES, Fresno. Everyone knows Los Angeles, but Fresno might be a bit less known to some readers. Fresno is a city in the central valley of California, much smaller in population size compared to Los Angeles (542,252 vs. 3,898,767 in April, 2020), and dominated by a goods producing economy. This second plot shows the simulation result for Fresno. Notice how much steeper the decline of employment is in comparison to the Los Angeles SES! Whereas the LA surface or employment dipped to around 94%, Fresno’s decline is down to 86%, suggesting a more severe impact of the open economy, or as we termed it, the “business-as-usual” policy. And this decline occurs despite the grey, disease-only surface seemingly no worse than that for LA.

The implication is that the economic cascade that would result from maintaining an open economy during COVID-19 in 2020 would have had more severe consequences for Fresno than it would have for LA. In the next post we will compare the results for all the California SESs, and explore the features of those socioeconomic systems driving the differences. Before that, however, I’ll leave you with this nifty alternative graphic of the simulation results. These plots, that look like wedges of cheese to me, are simply “fill-ins” of the gap between disease-only driven unemployment, and that driver plus the economic cascade. Lining up LA and Fresno side by side allows me to appreciate how differently the two SESs are predicted to respond. In the next post we’ll look at the cheese wedges for all the SESs, and compare them across the state.

Los Angeles-Long Beach-Glendale

Fresno

COVID-19, Economics, Tipping Points – Simulating an Outbreak

Tags

COVID-19, networks, real world networks, simulations, socioeconomics

Previous posts in this series:
1. COVID-19, Economics, Tipping Points – Part I
2. COVID-19, Economics, Tipping Points – Socioeconomic Networks
3. COVID-19, Economics, Tipping Points – All Models are Lies

Roopnarine, P. D., M. Abarca, D. Goodwin and J. Russack. 2023. Economic cascades, tipping points, and the costs of a business-as-usual approach to COVID-19. Frontiers in Physics. 11:1074704. doi: 10.3389/fphy.2023.1074704

Recap

In the last post we developed a network model of a typical American socioeconomic system (SES), and added dynamics to it in the form of differential equations. Those equations reflect the flow of economic goods and services (inputs and outputs) within and between all the industrial sectors in the network. Now this is very important: the model’s initial condition of the SES is one of equilibrium, i.e. all the flows are balanced, so that each sector or node in the network is stable regarding the number of persons employed in the sector. In other words, when we set the system into motion, it remains static. That system is boring (in a healthy sense), and a plot of any measure of economic health over time is simply a flat line (again in a healthy sense). And it will remain in this state in the absence of disease.

Disease outbreak

We can now make a qualitative prediction of the outcome of an outbreak of COVID-19 in the SES: some workers will become infected, some of those workers will either become too ill to remain employed, or will die, the demand for “raw” materials in that sector might fall (output certainly would), and the effects of the outbreak in that particular sector would therefore be transmitted, or cascade, to all other sectors. The sector would, at the same time, feel the impact of outbreaks in other sectors, as there would be multiple feedbacks generated in the system. This qualitative assessment leaves many questions unanswered though, and those questions get to the heart of why we set out on this investigation in the first place: How devastating would the economic downturn be if no action is taken to curb spread of the disease by shuttering the economy? The feedbacks complicate any simplistic attempt to answer the question, because there are both positive and negative feedbacks in motion. For example, a positive, or reinforcing feedback, will occur between two sectors that depend on each other; losses of workers to disease in each sector cause economic losses in the other sector, which in turn drives further losses in the first sector, and so on. A negative or dampening feedback would be the spread of the disease itself, which depends on transmission between infectious and susceptible individuals; the spread slows down as the number of susceptible persons–those who have not yet been infected–decreases, and hence contact becomes less probable.

Addressing the main question requires us to get quantitative, because we have to consider several important influencing factors, namely:
1. How intense is the outbreak? That is, at what rate is it spreading?
2. How many people are employed in the SES, and how are they divided up among the various sectors?
3. How healthy is the workforce, that is, how susceptible is it to the outbreak?

The answer to the first question is central to the study of communicable diseases, and great effort is put into estimating the rate of infection of any such disease. In the first post of this series we touched upon the basic SIR (Susceptible, Infected, Removed) model and showed that the increase in the number of infected/infectious persons is nonlinear, first accelerating with time, and then declining. To understand this, imagine that you are in a zombie apocalypse movie. Everyone knows that the zombification rate depends on the number of zombies: the greater the number of zombies, the faster the rate at which the number of zombies grow. In a real disease, both the number of suseptible and the number of infected persons will eventually decline, as susceptibles become infected and infected persons either recover, or do not. The figure at left illustrates this, showing an initial increase in the number of infected persons, with a peak, and then a slow decline.

We can apply this model easily to an SES if we have an initial rate of infection and an estimate of the number of people initially infected. We can also make our model a bit more nuanced by focusing on one feature of COVID-19 for which we had relevant demographic data, and that is the disease’s more severe impact on older persons. What that means for our model is that the impact on the labour force depends on the age structure of that sector, in that SES. And we incorporated that information into our model by breaking down each SES sector into four age categories, 5-17, 18-49, 50-64 and 65 years and over, and using the US CDC’s (Center for Disease Control) estimates of the rates of severe illness and fatality in each category.

Provisional COVID-19–Related Mortality Rates by Age Group and the Predominant Variant Period, United States, Weeks Ending January 4, 2020–October 1, 2022. (US CDC)

If you recall from the previous post, the dynamic model for each SES sector was written as

And now we make that a bit uglier by showing that

where n is one of our age sectors. All this equation says is that the rate of change of employees in a sector is a function of the rate, , at which workers are removed from the workforce (summed over all 15 sectors and 4 age categories). And that we measured as,

where d and h are death and hospitalization rates (again obtained from the CDC) for age category n, and |n| is the current size of or number of workers in n. N is the total size of the sector. What about R? Think of R for now as the estimated transmission rate. If R is greater than one, then it means that each infected/infectious person will spread the disease to at least one other person, probably more. If R is less than one, the disease dies out.

Perhaps the best way to show how this all works is to simulate it for an actual sector. Shown in these plots is the impact of the actual outbreak in March 2020, in San Francisco, for the Leisure and Hospitality sector (e.g. the hotel industry). We modeled the first 100 days of the outbreak, with an initial basic reproduction number, or R₀, of 1.5. This value was derived from numerous data and model sources at the time that were being actively compiled by the California Department of Public Health’s California COVID Assessment Tool (CalCAT). Take a look at the plots below. The plot on the left shows the results of the SIR model, and the corresponding loss of employees in the sector during the same time period is shown in the plot on the right. Note the nonlinearity of the response: there is initially very little impact, but the acceleration is rapid as infection in the population ramps up. Things eventually settle down as the disease runs its course through the population. Importantly, the reduction of the number of employees is not a one to one match with the disease, and you can see this by comparing the Susceptible curve on the left, to the employment curve on the right. The lack of correspondence is driven by the fact that employment depends not only on illness in the Leisure and Hospitality sector, but also illness and changes of employment levels (and hence productivity and demand) in all the other sectors.

Finally, we can break this result down and examine each age category individually. We see immediately the uneven impact of the disease across age brackets, a result all too familiar as we witnessed the terrible impact that the pandemic has had on older people. The projected losses of employment for those 65 and older in the Leisure and Hospitality sector would be greater than 30%, even though they comprised only 7.7% of people employed in the sector.

In the next post we will look more broadly at the ten Californian SESs, and whereas here we looked at the impact on different age groups, next we will examine the impact on economies of different sizes and structure.

COVID-19, Economics, Tipping Points – All Models are Lies

Tags

COVID-19, eugenics, Network theory, networks, real world networks, socioeconomics

Previous posts in this series:
1. COVID-19, Economics, Tipping Points – Part I
2. COVID-19, Economics, Tipping Points – Socioeconomic Networks

Roopnarine, P. D., M. Abarca, D. Goodwin and J. Russack. 2023. Economic cascades, tipping points, and the costs of a business-as-usual approach to COVID-19. Frontiers in Physics. 11:1074704. doi: 10.3389/fphy.2023.1074704

Useful Lies

There is a common saying among scientists that goes something like this: “All models are wrong, but some are useful”¹, or “…but some are less wrong than others” and so on, you get the point. I prefer, however, the title of this post, “All Models are Lies”, which I have shamelessly paraphrased (stolen) from the mathematician Eugenia Cheng, who has said that “all equations are lies” (and demonstrates the truth of that statement beautifully). Both statements are absolutely correct, in my opinion, when we interpret models or equations as representations of some aspect of reality; but that doesn’t mean that they are wrong, it simply means that we must be aware of the decisions that have been made when constructing the representations. Take for example the logistic equation as used to represent the growth of a biological population

EQ. 1: (POPULATION GROWTH RATE) = (INTRINSIC RATE OF INCREASE) x (POPULATION SIZE) x (GROWTH REGULATION)

Logistic growth. Population size is limited by carrying capacity, growing to that limit and remaining there. X(0) = 1, r = 1 and K = 100. That is, the environment can sustain up to 100 individuals of the species.

I derived and explained this equation, or model, in an earlier post. X is the size of the population, and dX/dt then is the growth rate, or the change of X as time passes. Logistic growth describes a pattern where the population grows very quickly when there are only a few individuals and therefore plenty of unused resources, but growth slows down as the population nears a level at which resources are becoming increasingly limited, and factors related to crowding can become an issue. This is a reasonably accurate description of how populations of organisms can grow, and as such the model describes the growth of population X with precision. BUT, X is not actually a population of actual organisms, it’s just a variable, and as such the equation is a lie; unless we choose to represent such a population with X. In doing so we are deciding explicitly to focus on the growth of the population as captured by the few variables in our equation, discarding many details that are either deemed irrelevant to that focus or that have minimal effects, or that are simply too difficult to incorporate into the current model. The inclusion of those details becomes increasingly difficult as the number of details to be considered increases, precision is elusive, and the result is more often than not a mathematical mess. The logistic equation is very useful, but we should never forget the fact that it is describing the growth of X, and that is useful to say an ecologist, only if and when we decide that X represents some aspect of the population of a biological species.

This is a bit of a conundrum in the world of complex systems, such as ecological or socioeconomic systems that involve numerous different players and masses of interactions. We can approach the problem with an extreme reduction of complexity, as in the example above, or as is possible with many physical systems. Let’s face it, throwing a ball and describing its dynamics with Newton’s laws of motion (simple equations) works great because we can usually ignore features like the surface texture of the ball or wind speed. Or we can approach things from the other direction and throw the kitchen sink at the problem and attempt to combine as many variables as can be measured and that might be involved in the system. For complex systems, perhaps the most reasonable approach is to find a point somewhere between these extremes where one can mobilize enough features that both describe the system sufficiently to yield some sense of realism, and that can be modeled reliably.

And I confess that this lengthy preamble is really intended to convince you of why we decided to model Californian socioeconomic systems (SESs) during the COVID-19 pandemic in the way that we did, and now that you’ve been convinced, let’s dive into the model. What we propose as our model is that an SES will remain unchanged in the absence of a COVID-19 outbreak.

The SES Model

Let’s look again at our network representation of the major industrial sectors in the typical SES, described in the previous post. All the sectors are connected because there are economic exchanges between them. Notice that the arrows linking sectors have different thicknesses. That is our graphical representation of the fact that the strength of the exchanges vary, with thicker arrows meaning that the recipient of goods or services (the direction of the arrow) is quite dependent on the donor. For example, many sectors depend heavily on Manufacturing, and hence there are many thick arrows flowing out of that sector. The flow of materials or money along those links, however, also depends on how much the donor sector (network node) is capable of producing and the demand from the recipient sector, and in our model we decided that both those factors are determined by the number of employees in each sector. In other words, if the Financial sector receives goods from Manufacturing, then the flow of goods depends on the ability of Manufacturing to produce those goods, and the demand from the Financial sector, and both of those depend on the number of labourers producing and demanding.

Our goal was to examine the effect that the pandemic would have on the network as the disease spread among workers in the sectors. In order to do that, we first had to bring our network to life, and we did that with the following bit of mathematics. First, we assumed that the growth rate of a sector, that is, the number of employees in the sector, is a function of the economic demands both within that sector, and from all other sectors in the SES network. Those demands in turn depend on both sector employment levels, as well as the strength or value of the exchanges between sectors. Second, we modeled the outbreak of COVID-19 in the general population of the SES, and applied that to each sector. Let’s break this down into steps and derive the model.

Let’s assume that a sector, i, is independent of all the others, and that workers in the sector suffer an outbreak of disease. Then the growth rate of the sector may be expressed simply as

EQ. 2: RATE OF CHANGE OF EMPLOYEES = (RATE OF EMPLOYEES LOST TO DISEASE) x (NO. OF EMPLOYEES)

where is the number of employees in i, and is the rate at which workers are being lost–in that sector. We assume that workers are lost either to fatality, or because they suffer severe illness and are no longer able to work. We also assume that no new employees are being added, which was largely true at the beginning of the lockdowns, and therefore that the growth rate is always zero (if there is no disease then ) or negative ().

This is straightforward enough, but we want to capture the network by adding the interactions and inter-dependencies with the other sectors to our equation. We do that by first figuring out how much each interaction is worth, and that we did using something known as the “industry by industry total requirement” or input-output exchanges, which is kindly provided to us by the United States by the US Bureau of Economic Analysis (yet another good use of taxes employing government workers!). We then weighted each interaction (network arrow) by how much it was worth relative to the total interactions or exchanges for a sector. The dependency of sector i on sector j can now be expressed as the sum of what i provides to j, and what j provides to i.

EQ. 3: RATE OF CHANGE OF EMPLOYEES = (RATE OF EMPLOYEES LOST TO DISEASE) x (NO. OF EMPLOYEES) x (INPUT-OUPUT EXCHANGES WITH SECTOR j)

where is the relative weight of the flow from i to j ( refers to exchanges within sector i itself). The value of the exchange is this weight multiplied by the number of employees in sector j at time t () relative to the original number of employees (at time 0).

Whew! I know that this is a mouthful, but there is one final step, and that is to sum the above exchanges over all the sectors in the SES network, which gives us this somewhat scary formula.

EQ. 4: RATE OF CHANGE OF EMPLOYEES = (RATE OF EMPLOYEES LOST TO DISEASE) x (NO. OF EMPLOYEES) x (THE SUM OF ALL INPUT-OUPUT EXCHANGES WITH SECTOR i)

Thankfully, with a little algebra we can simplify it to

where represents the value of exchanges between sectors. Really, all the equation says is: THE SOCIOECONOMIC SYSTEM WILL REMAIN IN EQUILIBRIUM UNLESS WORKERS ARE REMOVED FROM ANY SECTOR BECAUSE OF ILLNESS OR DEATH. This should be obvious, because in the absence of COVID-19, , so everything on the right hand side of the equation will also be zero, and therefore the rate of change of workers employed in sector i will also be zero. A static system.

If the notion of a static economic system appears to be a bit unreal, that’s because it is. This bothered several economists who reviewed our paper, but I would argue that they were missing the point of both a useful mathematical model, as well as the counterfactual basis of our model. We could introduce a bit of numerical noise to mimic fluctuations in the market, consumer activity and so on, but we are assuming that those average out on the short-term, and would add unnecessary complications to the analysis. Remember that the goal of the model is to address the question of what would have happened if an SES was allowed to continue operating without any economic shutdown. In the next post we will develop a way to do precisely this, by poking the system with simulated outbreaks of COVID-19.

¹Attributed to the accomplished 20^th century statistician, George Box. I hesitated to cite him, as I am uncertain if Box subscribed to the eugenics movement prevalent among many British and American statisticians of the era. I simply don’t know, but I do know that he was the son-in-law of Ronald Fisher, one of the century’s most accomplished statisticians, and also a notorious eugenist. Box also made reference in his own work to papers published in the discredited Annals of Eugenics (to which I will not provide a link).

COVID-19, Economics, Tipping Points – Socioeconomic networks

Tags

COVID-19, Network theory, networks, socioeconomics

Previous posts in this series:
1. COVID-19, Economics, Tipping Points – Part I

Roopnarine, P. D., M. Abarca, D. Goodwin and J. Russack. 2023. Economic cascades, tipping points, and the costs of a business-as-usual approach to COVID-19. Frontiers in Physics. 11:1074704. doi: 10.3389/fphy.2023.1074704

Complex Systems

An aquatic food web. doi:10.3389/frym.2018.00004

A system, meaning a group of interacting elements (in turn meaning anything really), is considered to be complex if it displays certain properties that make its behaviour hard to predict, including adaptation, path-dependence (history matters) and emergence. Elements, entities, agents, whatever you wish to call them, are often adaptable to changing conditions. For example, one of the core discoveries of evolutionary theory is that populations of species are capable of adapting to a changing environment via natural selection, if there is sufficient genetic variation. The adaptability of a complex system is a bit more difficult to understand because, while it is rooted in the adaptive dynamics (I prefer “dynamics” to the more often used “behaviours”; it is more accurate) of its elements, it is at least the sum of all those individual adaptive dynamics, and quite often is more: “the whole is more than the sum of its parts” (or, as Aristotle said it originally: “the whole is something besides the parts). That is, the system will display properties that are neither shared with any of its constituent elements, nor are they easily predicted from elemental properties. Such system-level properties are termed “emergent”.

There are unfortunate tendencies on the one hand to treat emergent properties as mysterious or inaccessible, or on the other, as the failure of an observer to reduce them to the level of the elements. Neither is correct. An “elementary” example is water: the macroscopic properties of water, e.g. wetness, or turbulence, or being denser in its liquid form compared to its solid form (ice floats; see this blog’s banner image!), are not easily predicted from the properties of atomic hydrogen and oxygen. Yet great progress can be made from understanding how the molecular combination of two hydrogen atoms and one oxygen atom interact with each other. Complex systems can be very sensitive to initial conditions, meaning both that limited precision in understanding those initial conditions, and that their histories can dictate to a great extent their futures, places limits on our ability to simply list the parts and relationships of its system and then predict its possible future. (I refer readers interested in complexity and complex systems to the excellent and accessible volume, “Signs of Life” by Ricard Sole and Brian Goodwin).

What does this all have to do with economics during the time of COVID-19? In my previous post I explained that our investigation was motivated by prior work on ecosystems and mass extinctions. Ecosystems are complex systems, and their responses to extreme stresses, such as during times of mass extinction, can appear to be unpredictable. Nevertheless, our treatment of ancient ecosystems as complex networks of interacting species have allowed us to make predictions consistent with the fossil record. For example, we have uncovered multiple phases of the end Permian extinction in both terrestrial and marine systems, and the unique dynamics of systems in the aftermath of the extinction. The key to unlocking ecosystem properties lies in treating the systems as complex networks of interactions, and there is a long history in theoretical ecology rooted in the foundational work by Robert May back in the 1970s. May was also a proponent of treating economic systems in the same manner, recognizing that such systems possess complex dynamics.

An Economic Network

It was with this in mind that we approached our counterfactual question of whether shutting down economies early in the COVID-19 pandemic would have avoided the subsequent extreme reductions of productivity and losses of employment. To my knowledge, studies of the economy during this time have followed three general paths. First, there have been fascinating studies at the level of individuals, facilitated by both “big data” and computational power. For example, Serina Chang (Stanford University) and colleagues examined responses to the chaos of those months early in 2020 by accessing population movement based on cell phone signals. A second path appears, to my untrained economist eye, as more conventional analyses of economic indicator data, such as tracking monetary or products flows and making predictions based on economic theory. I will confess that I am uncomfortable with conventional theory which treats any complex system, including the economy, with notions of equilibria, predictability, and linear mathematics; see work by Brian Arthur. They don’t appear to correspond very closely to the real world.

The third approach, ours, was to combine network views of economies with the type of mathematical modeling that has been used to examine complex systems in other areas, including ecology and physical systems. Our goals were straightforward. First, construct a network of relationships among various economic entities; second, develop a mathematical model of the economic interactions among those entities; and third, simulate the response of the network to an outbreak of COVid-19 in which no attempt was made to tackle the outbreak by disrupting the economic interactions.

A California Network

We decided to focus on the US state of California for several reasons. First, three of us live in California, and back in 2020 were experiencing first hand the impact of the pandemic and economic shutdown here. California also has a very diverse economy, being both the largest agricultural producer in the nation, and a hub for financial, technological and entertainment industries. Finally, it possesses one of the world’s largest economies, ranking fifth in 2019, ahead of many nation states. Therefore, we felt that California could be representative of a broad range of other places. This diversity in California, however, also meant that it would be a mistake to treat the state as a single, homogeneous system. We got around this by taking advantage of a system of geo-economic partitioning used by the United States Bureau of Labor Statistics (USBLS), wherein the United States is divided into metropolitan divisions or metropolitan statistical areas for the purposes of collecting Federal statistics, including economic. In total we considered ten major metropolitan areas in California (see map), and for each we compiled population size and the size of the employed labour force. We referred to each area as a socio-economic system (SES).

We divided the economy within each SES into a set of 15 major economic or industrial sectors, following a major classification system used by both the USBLS and the California Employment and Development Department (CAEDD). All these sectors are networked, or connected to each other because each sector both depends on the others, as well as provided goods or services to others. For example, the agricultural sector obviously provides food to workers in all other sectors, but it needs goods produced by Manufacturing, and it depends on Transportation, as well as Health and Leisure. In ecology we would consider this to be a mutualistic network. The connections or links between the networks are more than just symbolic of these exchanges though; they also possess magnitude, that is, the strengths of the inter-sector dependencies. We measured these using the average monetary exchanges between sectors, or inter-industry exchanges, as measured by the US Bureau of Economic Analysis.

The end result was that we now had a network showing the breakdown of our economy into semi-independent entities, as well as the relationships among those entities. That network, when populated with employees and monetary values from a particular place, becomes a model of the economic system of that place. All that was needed next was to make the system dynamic, basically bringing it to life with mathematics, and initiating the pandemic. I’ll describe those steps in the next posts!

COVID-19, Economics, Tipping Points – Part I

Several colleagues and I recently published a paper in the journal Frontiers in Physics. The paper is a trans-disciplinary (read “mashup”) fusion of our work on ecological complexity, networks and mass extinctions, with economics and the COVID-19 pandemic. Our goal was to tackle the contentious question, “Would economies have fared better during the worst stages of the pandemic if there had been no shutdowns?” This post and the following series will relate how and why we conceived the idea, developed a model to test the question, and what we discovered.

The setting

It was April, 2020, and much of the world was in various states of shutdown because of the COVID-19 pandemic. There were no effective treatments, and no vaccines. The disease was raging out of control in many areas, such as New York City and northern Italy, and threatening to overwhelm health services in many more. The best strategy under such circumstances, and the one underlying mandates or recommendations for social distancing, masking, and the shutdown of non-essential businesses and services, is to slow or disrupt the spread of the disease. The spread of a contagious disease can be modeled in a simplistic, yet effective way by the now famous SIR (Susceptible, Infected, Removed) model. Here the spread to susceptible persons, those who have not yet contracted the disease, is a function of the probability of contact with an infected and contagious individual, and the probability of contracting the disease via contact.

EQ. 1: RATE OF CHANGE OF THE NUMBER OF SUSCEPTIBLE PERSONS = (PROBABILITY OF INFECTION) x (NUMBER OF INFECTIOUS PERSONS) x (NUMBER OF SUSCEPTIBLE PERSONS) / (TOTAL POPULATION SIZE)

where S is the number of people out of a total population size N, who are susceptible to the disease. I is the number of persons who are infectious, and is the average number of contacts of an infected individual per unit time (t). The negative sign indicates that the number of susceptible or uninfected individuals declines over time, and therefore conversely

EQ. 2: RATE OF CHANGE OF THE NUMBER OF INFECTIOUS PERSONS = (INCREASE IN NUMBER OF INFECTIOUS PERSONS; see above) – (NUMBER OF INFECTIOUS PERSONS REMOVED)

where is the rate at which individuals are removed from the “infected pool”, either by recovery, or by death. Thus you can see that reducing by any means both reduces the rate at which the infected pool grows, and the susceptible pool declines. You can view the output of this model in the figures below. The blue lines represent the fraction of susceptible persons at the beginning of an outbreak of a hypothetical infectious disease. The red lines show the fraction of infectious persons, set initially at a very low 0.0002%, or 2 out of a million. Time passes, and the number of infectious individuals increases as the disease spreads, and therefore the number of individuals who have not been infected declines. The rate of infection is greater for the scenario and plot on the right, hence the steeper slopes of the blue and red lines. The lower rate of infection on the left could be the result of mitigating actions, such as social distancing and masking, with a slower progression of the disease, and fewer overall infections. Both of those outcomes would be desirable from the standpoint of health services.

Reducing the rate of infection with mitigating actions is easy enough to state in words and mathematics, but proved much more controversial when actually put into practice in early 2020. One of the most controversial actions taken by authorities in the United States was the closure of non-essential businesses, essential businesses being those involved in health care, food services and the like. The economic impact was severe, with unemployment rates skyrocketing across the country, indeed the globe. To be clear, many of the layoffs by April were not the result of a downturn of economic activity, because insufficient time had elapsed for that. Instead, many workers were released because of the anticipated downturn, anticipated because of reduced economic activity. That triggered a vicious cycle of positive feedback, accelerating the anticipated downturn, amplifying fears, more layoffs and so forth. This sort of positive feedback appears to be common in economies, with recent examples being the failure of several large banks in the United States because of “bank runs”; one bank fails, triggering fears among individuals with large holdings in similar banks, those individuals withdraw large sums in a short period of time, the bank’s resources are stretched, triggering more fears, etc. By the way, a dominant role of positive feedback in economic markets, often triggered by individual behaviours, runs somewhat counter to the conventional theory of markets being governed by rational decision making, and equilibrium dynamics. Clearly an area of theory in need of an overhaul.

Theory aside, the economic hardships endured in early 2020 were real, whether it was a loss of employment, or a reduction of income, and it generated a significant backlash against shutdown policies. This included a tremendous amount of hyperbole by economists, political pundits and the like, with some even claiming that a shuttered economy would kill tens of thousands of Americans, many more than the disease itself. Hyperbole indeed, given that more than one million Americans have died because of COVID-19.

Germ of an idea

It was at this time that a friend, David Goodwin, and I had a conversation. Dave is a professor of geosciences at Denison University in Ohio, and one of our common interests is the histories of human societies, viewed as complex systems. He raised the question of the similarity between cascading effects of the shutdown on an economic system, and the cascading effects of perturbations to ecological systems. The latter is something that I’ve spent a great deal of time thinking about, as readers of this blog are aware. Unlike ecological catastrophes such as mass extinctions, however, we would not have to dig into an incomplete geological record to reconstruct past events. We could simply wait and watch them unfold. So the effects of the shutdown would eventually become apparent to us. But, we would never answer the question, “What would have happened if we did not shutdown the economy?” Perhaps opponents of the policy were correct. How would we ever know? That is when I decided to construct a counterfactual scenario.

A counterfactual event is one that did not happen, but could have happened. For example, maybe it didn’t rain today, but one could certainly explore what could have happened if it indeed had rained. Counterfactuals are those “What if…” questions that belong to realm of didn’t happen, but could have happened. After spending a weekend unable to get our conversation off my mind, I gathered together a small team of collaborators, including Dave, Maricela Abarca, a data scientist at the California Academy of Sciences, and Joe Russack, a programmer also at the Academy. And what we did was to ask the following question: “What would have happened to California’s economy if the government did not shutter the economy in March 2020?” What followed was an exercise in grant writing, data gathering, mathematical model building, and a bit of doggedness squaring off against conventional economics. I will describe our study in this series of posts, but for a preview, you can check out the paper that resulted from all this. The paper does have its fairly technical bits of course, but diving in and explaining it in plain language is the goal of this blog series. You can also check out a nice media-friendly, plain language summary here.

Being an Optimist – Earth Day 2023

It has been more than one year since my last post on the blog. I apparently needed a break from somethings, as I think has been the case for many as we emerged from the first phase of the ongoing COVID-19 pandemic. I was running errands early this morning though, and after weeks and weeks of historic winter storms and rains, Berkeley and the rest of the San Francisco Bay Area is a riot of green and fantastic colours. The sunshine is brilliant today, and as I looked at all the natural colours around me, and the crazy-coloured houses and people, I thought, what a wonderful chaotically diverse and complex planet this is. Definitely the envy of the Solar System.

Now I have a lot to blog about(!), and I thought that I would begin with a short talk that I gave this week at San Francisco State University, celebrating Earth Day (they celebrate Earth Week!). I participated in STEAM Day, hosted by the university’s Climate HQ, and included folks from our Geology Department at the California Academy of Sciences, the SETI Institute, the Astronomical Society of the Pacific, and UC Berkeley’s American Indian Graduate Program, among others. (Did you know that Earth Day was conceived at a UNESCO meeting right here in San Francisco in 1970?) I had very little idea what I would talk about, until perhaps 18 hours before the event. But, sitting and looking at the view outside my living room window, I realized that even though I spend much of my time in the gloomy (but super interesting) world of extinctions, ecological collapses, and Anthropocene crises, I remain optimistic about the future. Therefore, I spoke for a few minutes, and tried to convey both the seriousness of our present situation, and why I still remain an optimist. I don’t think that I succeeded in explaining the latter very well, but standing on the dais in Malcolm X Plaza on the SFSU campus, here’s more or less what I had to say.

I am a scientist who focuses on issues of global ecological and evolutionary change. My specialty is paleontology, and I’ve done a lot of work studying ancient ecosystems to understand how they have responded to past calamities, such as the well known asteroid impact 66 million years ago, and the perhaps less well known episodes of extreme climate change. Studying the past gives us a window into our possible future, as we struggle to understand what is in store for ourselves and the rest of the planet over the next several decades and centuries. The view from that window is often an uncomfortable one because I tend to focus on ancient extreme events, particularly those that resulted in mass extinctions. The reason for focusing on extreme changes is because those stressful situations often give us the most insight into how large, diverse and complex systems function and respond to changes. The general conclusions that I draw from my work of many years on this topic are that ecosystems are generally very stable when they are the products of species interacting and coevolving over very long periods of relative environmental calm. That stability can make them remarkably resilient against environmental changes and disruption, such as global warming, but, ultimately they have tipping points. That is, there is a level of disruption associated with every type of disruption and ecosystem that can cause the ecosystem to collapse, usually in a cascade of extinctions. Nevertheless, time and again as this has happened in our planet’s history, ecosystems have either recovered, or new ones have arisen to take their place and begin the cycle all over again.

The discomfort that I get from this type of work is rooted in the insight that it gives me into our possible future. The global environment today is changing more rapidly than at any time in at least the past 500 million years, with the exception of the asteroid impact 66 million years ago. Furthermore, the drivers of change today present novel ecological and evolutionary challenges to species and ecosystems because they are human-caused. The major drivers of change are habitat or landscape alteration or destruction; invasive species; species over-exploitation; pollution; and of course global climate change. Now, most of these do have natural analogs. For example, geological processes alter landscapes all the time on multiple timescales, ranging from the very slow processes of plate tectonics and continental drift, to rapid events such as major earthquakes and catastrophic floods. As another example, invasive species are largely the result of species being moved to areas outside of their natural geographic ranges because of human activities, both intentional and unintentional, and those species can have very negative impacts on resident species and their habitats. But the geographic dispersal of species is also a natural process, facilitated by species capabilities, as well as geological processes, such as the removal of physical barriers. For example, the last time that the Arctic Sea was ice free, over a million years ago, there was a massive invasion of the North Atlantic by species from the North Pacific. And the effects of that natural biotic invasion reverberate today even as a new invasion is underway.

The fact that habitat alteration and species movements occur naturally, however, doesn’t make it okay for humans to do those things because there are several important differences. First, in nature there is generally a tradeoff among pace, intensity and frequency, in that very intense or high magnitude events tend to occur less frequently and more locally, such as a severe earthquake. In contrast, a global alteration such as continental drift is significantly slower. The human analogs, on the other hand, are mostly frequent, intense and increasingly globally pervasive.

Similarly, pollution and climate change also have natural ancient analogs. The end Permian mass extinction that occurred 251 million years ago is the most severe mass extinction recorded in the geological record, and is one of the topics on which I do a lot of research. Somewhere between 80-90% of known species became extinct. It appears that terrestrial extinctions happened slightly earlier than the marine ones, but the whole process lasted at most 100,000 years, and probably occurred in considerably less time. It was caused by unbelievably massive volcanism in what is now Siberia, and this volcanism altered the chemistry of both the atmosphere and the oceans, i.e. pollution, and caused significant changes of climate, such as ocean warming and widespread drought. Sound familiar? Research conducted by myself and colleagues suggests that it might have taken as long as 5-7 million years for terrestrial ecosystems to begin functioning properly once again.

Now, as a scientist at the Academy, I talk about these things often with the public and students, and there is one question that I am almost always asked, and that is, “Are you optimistic about our future?” That’s a very difficult question to answer, because it hinges on my ability to predict the future, and when it comes to that, I am guided one known, and one unknown. The known is this: based on our studies of past events, our understanding of how the planet functions, and the impacts of our actions, we know that we are losing biodiversity and that the rate of extinction is accelerating. These will continue into the foreseeable future, partly because there are changes now underway that will be difficult to reverse, notably climatic changes. However, the current rate of extinction is also such that, in my opinion, we are not yet into a mass extinction. Mass extinctions are truly overwhelming events. Pause for a moment… think about a world where 70-90% of all the species that you know are no longer here. That is a staggering thought about a very different world. We might be on the threshold of a mass extinction, but we’re not quite there yet. 

And that brings me to the unknown. Whereas in the past, species were subjected to planetary or even extraterrestrial events and processes, today’s crisis is the result of the actions of a single species. And that species, ourselves, is a conscious and self-aware one. We examine our actions and their consequences all the time, and while we are currently perhaps too slow, and sometimes unwilling to do the things that we know must be done to preserve our planet, it is truly remarkable that we have both the knowledge and the self-motivation to act: witness that right now, we are all gathered here today to celebrate our Earth. All around the world, people are celebrating Earth Day, and every day are taking more positive action. That makes me optimistic. I truly believe that humans and our societies are capable of rapid and meaningful change. I am happy to remain ignorant of where our collective actions will leads us, because I sincerely believe that it will be toward a healthier planet and a better world. Happy Earth Day everyone.

Rates of Evolution – Palaeontology’s greatest ever graphs

Tags

evolution, paleontology, rates of evolution

The Palaeontological Association has been running a fun series of essays in its newsletter entitled “Palaeontology’s greatest ever graphs”. I was kindly invited by the editor Emilia Jarochowska to write the latest essay, which featured this iconic graph published by Phil Gingerich in 1983 (wonderfully recreated and cartoonified by Ratbot Comics). The figure compiled data on measured rates of morphological evolution, plotting them against the interval of time over which the rate was measured. In other words, say I measured the rate of evolution of a species of snail every generation, and generations last one year, I would then plot those rates against one year. When Gingerich compiled rates ranging over intervals spanning days to millions of years, he got the inverse relationship (negative slope) shown in the figure. In other words, the longer the interval of time, the slower the measured rate! Debate raged over whether this was an actual biological feature, wherein rates at different times could differ greatly, or whether it was some sort of mathematical, or even psychological artifact. Well, here’s my take on it. And if you like the figure, head over to Ratbot Comics where you will find some truly fun stuff from the artist, Ellis Jones. Enjoy.

Inverse relationship of evolutionary rates and interval of time over which rates were measured

The rates at which morphological evolution proceeds became a central palaeontological contribution to development of the neo-synthetic theory of evolution in the mid-twentieth century (Simpson, 1944; Haldane, 1949). Many decades later we can say retrospectively that three questions must qualify the study of those rates. First, how is rate being measured? Second, at which level or for what type of biological organization is rate being measured, e.g. within a species or within a clade (Roopnarine, 2003)? Third, why do we care about rate? In other words, what might we learn from knowing the speed of morphological evolution?

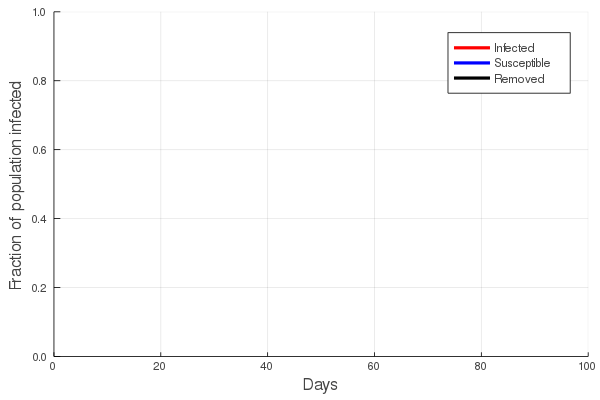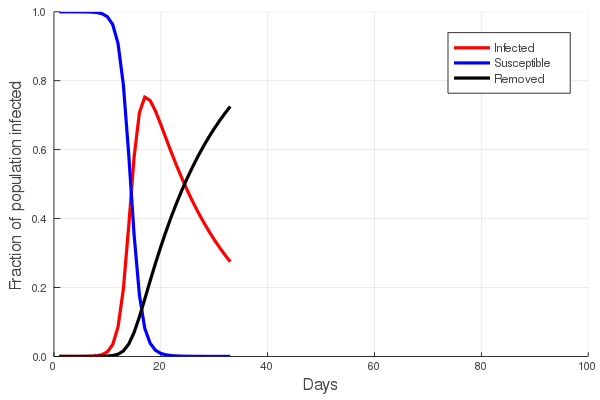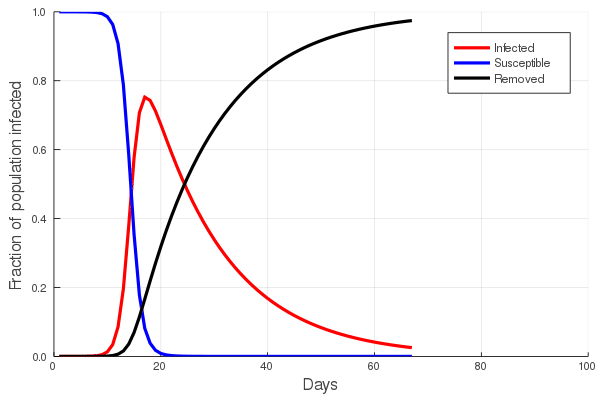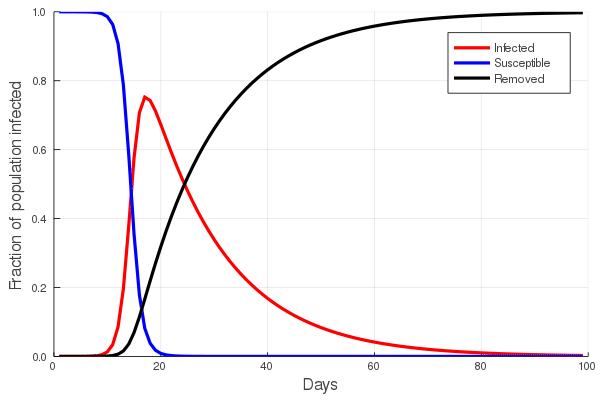
The figure presented here illustrates a compilation of rates of morphological evolution calculated within species, or within phyletic lineages of presumed relationships of direct ancestral- descendant species (Gingerich, 1983). The most obvious feature is the inverse relationship between rate and the interval of time over which a rate is measured. The compilation included data derived from laboratory experiments of artificial selection, historical events such as biological invasions, and the fossil record. The rates are calculated in units of “darwins”, i.e., the proportional difference between two measures divided by elapsed time standardized to units of 1 million years (Haldane, 1949). This makes 1 darwin roughly equivalent to a proportional change of 1/1000 every 1,000 years. Haldane’s interest in rates was to determine how quickly phenotypically expressed mutations could become fixed in a population, and he expected the fossil record to be a potential source of suitable data. Later, Bjorn Kurtén (1959), pursuing this line of thinking was, I believe, the first to note that morphological change, and hence rate, decreased as the interval of time between measured points increased. Kurtén, who was measuring change in lineages of mammals from the Tertiary, Pleistocene and Holocene, throughout which rates increased progressively, suggested two alternative explanations for the inverse relationship: (1) increasing rates reflected increasingly variable climatic conditions as one approached the Holocene, or (2) the trend is a mathematical artifact. Philip Gingerich compiled significantly more data and suggested that the decline of rates as measurement interval increases might indeed be an artifact, yet a meaningful one. To grasp the significance of Gingerich’s argument, we must dissect both the figure and Kurtén’s second explanation.

The displayed rates vary by many orders of magnitude, and Gingerich divided them subjectively into four domains, with the fastest rates occupying Domain I and coming from laboratory measures of change on generational timescales. The slowest rates, Domain IV, hail exclusively from the fossil record. Kurtén suggested that, as the geological span over which a rate is calculated increases, the higher the frequency of unobserved reversals of change. Thus change that might have accumulated during an interval could be negated to some extent during a longer interval, leading to a calculated rate that is slower than true generational rates. Gingerich regressed his compiled rates against the interval of measurement, and not only validated Kurtén’s observation for a much broader set of data, but additionally asserted that if one then scales rate against interval, the result is unexpectedly uniform. This implies no difference between true generational rates, rates of presumed adaptation during historical events, and phyletic changes between species on longer timescales. It is a simple leap from here to Gingerich’s main conclusion, that the process or evolutionary mode operating within the domains is a single one, and there is thus no mechanistic distinction between microevolutionary and macroevolutionary processes.

Perhaps unsurprisingly, the first notable response to Gingerich’s claim was made by Stephen Gould (1984), a founder of the Theory of Punctuated Equilibrium, and a major force in the then developing macroevolutionary programme. A major tenet of that programme is that there exists a discontinuity between microevolutionary processes that operate during the temporal span of a species, and macroevolutionary processes that are responsible for speciation events and other phenomena which occur beyond the level of populations, such as species selection. Gould objected strongly to Gingerich’s argument, and presented two non-exclusive alternative explanations. Appearing to initially accept a constancy of rate across scales, Gould argued that the inverse relationship between rate and interval must require the amount of morphological change to also be constant. He found Gingerich’s calculated slope of 1.2, however, to be suspiciously close to 1, pointing towards two psychological artifacts. First, very small changes are rarely noticed and hence reported, essentially victims of the bias against negative results. Second, instances of very large change tend to be overlooked because we would not recognize the close phyletic relationship between the taxa. This second explanation strikes directly from the macroevolutionist paradigm. Gould proposed that the very high rates measured at the shortest timescales (Domain I) are a biased sample that ignores the millions of extant populations that exhibit very low rates. This bias creates an incommensurability with rates measured from the fossil record, which would be low if morphological stasis is the dominant mode of evolution on the long term.

Gingerich and Gould, observing the same data, arrived at opposing explanations. Neither party, unfortunately, were free of their own a priori biases concerning the evolutionary mechanism(s) responsible for the data. A deeper consideration of the underlying mathematics reveals a richer framework behind the data and figure than either worker acknowledged. Fred Bookstein (1987) provided the first insight by modelling unbiased or symmetric random walks as null models of microevolutionary time series. Bookstein pointed out that for such series, the frequency of reversals is about equal to the number of changes in the direction of net evolution between any two points. In other words, if a species trait increased by a factor of x when measured at times t₁ and t₂, the number of generations for which the trait increased is roughly equal to the number of generations for which it decreased (in the limit as series length approaches infinity). “Rate” becomes meaningless for such a series beyond a single generational step! In one fell swoop, Bookstein rendered the entire argument moot, unless one could reject the hypothesis that the mode of trait evolution conformed to a random walk. He also, however, opened the door to a better understanding of the inverse relationship: measures of morphological change over intervals greater than two consecutive generations cannot be interpreted independently of the mode or modes of evolution that operated during the intervals.

In order to understand this, imagine a time series of morphological trait evolution generated by an unbiased random walk. That is, for any given generation the trait’s value, logarithmically transformed, can decrease or increase with equal probability by a factor k, the generational rate of evolution. The expected value of the trait after N generations will be x₀±kN^0.5 (see Berg, 2018 for an accessible explanation), where x₀ is the initial value of the trait. Selecting any two generations in the series and calculating an interval rate then yields (x_N-x₀)/N = kN^0.5/N = kN^-0.5. Logarithmic transformation of the interval, as done in the figure, will thus yield a slope of -0.5. Alternatively, suppose the mode of evolution was incrementally directional (a biased random walk), then the expected rate would simply be kN^a, where a>-0.5. The expected rate generated by a perfectly directional series would be kN⁰, yielding a slope of rate versus interval of 0 (I’ll leave the proof to readers; or see Gingerich, 1993 or Roopnarine, 2003). And finally, a series that was improbably constrained in a manner often envisioned by Gould and others as stasis (Roopnarine et al., 1999), would yield a slope close to -1. Gingerich (1993) exploited these relationships, using all the available observations from a stratophenetic series to classify the underlying mode, and presumably test the frequency with which various modes account for observed stratophenetic series: slope 0 – directional, ~-0.5 – random, -1 – stasis. The method suffered complications arising from the regression of a ratio on its denominator (Gould, 1984; Sheets and Mitchell, 2001; Roopnarine, 2003), and the fact that the statistics of evolutionary series converge to those of unbiased random walks as preservational incompleteness increases (Roopnarine et al., 1999). It is nevertheless intimately related to the appropriate mathematics (Roopnarine, 2001).

Ultimately, we can use these relationships to understand that the inverse proportionality between rates and their temporal intervals is compelled to be negative because of mathematics, and only mathematics. Given that no measures of morphology are free of error, and that it is highly improbable that any lineage will exhibit perfect monotonicity of evolutionary mode during its geological duration, then all slopes of the relationship must lie between -1 and 0. Furthermore, the distribution of data within and among the four domains by itself tells us very little about mode, for it consists of point measures taken from entire histories, and those measures cannot inform us of the modes that generated them. Gingerich’s method (1983, 1993) might have been problematic, but it provided a foundation for further developments that demonstrated the feasibility of recovering evolutionary mode from stratophenetic series (Roopnarine, 2001; Hunt, 2007). Perhaps it is time to circle back to this iconic figure and broadly reassess the distribution of evolutionary rates in the fossil record (Voje, 2016).

References

BERG, H. C. 2018. Random walks in biology. Princeton University Press, 152 pp.
BOOKSTEIN, F. L. 1987. Random walk and the existence of evolutionary rates. Paleobiology, 13 (4), 446–464.
GINGERICH, P. D. 1983. Rates of evolution: effects of time and temporal scaling. Science, 222 (4620), 159–161.
GINGERICH, P. D. 1984. Response: Smooth curve of evolutionary rate: A psychological and mathematical artifact. Science, 226 (4677), 995–996.
GOULD, S. J. 1984. Smooth curve of evolutionary rate: a psychological and mathematical artifact. Science, 226 (4677), 994–996.
HALDANE, J. B. S. 1949. Suggestions as to quantitative measurement of rates of evolution. Evolution, 3 (1), 51–56.
HUNT, G. 2007. The relative importance of directional change, random walks, and stasis in the evolution of fossil lineages. Proceedings of the National Academy of Sciences, 104 (47), 18404–18408.
KURTÉN, B. 1959. Rates of evolution in fossil mammals. 205–215. In: Cold Spring Harbor Symposia on Quantitative Biology Vol. 24. Cold Spring Harbor Laboratory Press.
ROOPNARINE, P. D. 2001. The description and classification of evolutionary mode: a computational approach. Paleobiology, 27 (3), 446–465.
ROOPNARINE, P. D. 2003. Analysis of rates of morphologic evolution. Annual Review of Ecology, Evolution, and Systematics, 34 (1), 605–632.
ROOPNARINE, P. D., BYARS, G. and FITZGERALD, P. 1999. Anagenetic evolution, stratophenetic patterns, and random walk models. Paleobiology, 25 (1), 41–57.
SHEETS, H. D. and MITCHELL, C. E. 2001. Uncorrelated change produces the apparent dependence of evolutionary rate on interval. Paleobiology, 27 (3), 429–445.
SIMPSON, G. G. 1944. Tempo and Mode in Evolution. Columbia University Press, 217 pp.
VOJE, K. L. 2016. Tempo does not correlate with mode in the fossil record. Evolution, 70 (12), 2678–2689.